这是一个 Morris 计数器（近似计数算法）的 Java 实现，用很小的数据结构准确估计具有几十亿数据量的数据计数。 我们通常会定义一个 Long 类型对象，通过累加的方式实现计数。每个 Long 类型占用 8 byte (64bit) 空间，如果你有 30 亿个要记录的对象，那么你就需要 22GB 的空间存储这些计数器，这还不不包括在哈希中的对象ID。

背景

近似计数算法是允许我们使用非常少量的内存对大量事件进行计数的技术。它由 Robert Morris 于 1977 年发明。 该算法使用概率技术来增加计数器，尽管它不能保证准确性，但它确实提供了对真实值的相当好的估计，同时引入了最小但相当恒定的相对误差。 在这篇文章中，我们详细介绍了 Morris 算法及其背后的数学原理。

Morris 在贝尔实验室工作时遇到了一个问题。他应该编写一段代码来计算大量事件，而他只有一个 8 位计数器。 由于事件的数量很容易超过 256，使用普通方法计算它们是不可行的，这种限制导致他构建了这个近似计数器，它不是提供精确计数，而是提供一个近似计数。

计数和投硬币

构建近似计数器的一个简单方案是对每次事件变换进行计数。每收到一个新事件，我们抛一次硬币，如果正面朝上，我们增加计数，否则不增加。 这样计数器中的值平均下来将代表总事件的一半（因为抛硬币的获得正面并的概率是 0.5）。当我们将计数乘以 2 时，我们将得到近似实际数量的计数。

CoinFlipsCounter.java

这种基于抛硬币的计数技术是参数为 (n, p) 的二项分布，其中 n 是所见事件的总数，p 是成功概率，即在抛硬币过程中出现正面的概率。对真实事件数 n 的计数值 v 由下式给出

$$ \large 估算值v = 实际值n * 概率p = 实际值n/2 $$

这种二项式的正态分布标准偏差将帮助我们找到估算中的误差，对于正态分布平均值两侧标准差的两倍覆盖了分布的 95%；我们使用它来查找计数器值中的相对和绝对误差。

$$ \large 误差 = \sqrt{实际值n * 概率p(1-概率p)} = \sqrt{估算值v/2} $$

例如：估算计数器的值是 200，那么我们可以生成的最接近实际事件数量的近似值是 2 * 200 = 400。尽管 400 可能不是实际看到的事件数量，我们可以说，有 95% 的置信度。 根据上边的公式可以得出误差为 10。

$$ \large \sqrt{200/2} = 10 $$

我们根据 正态分布平均值两侧标准差的两倍覆盖了分布的 95% 这一规律计算，估算值为 200 正负 2*10 这个范围

$$ \large 估算值v \approx [180, 220] $$

那么真实值范围就是

$$ \large 真实值n \approx [360,440]$$

有了这个简单的抛硬币计数器，可以让我们的计数能力翻倍。通过改变 p 的值，这种方法可以扩展到计算更大的数字。这里观察到的绝对误差很小，但对于较小的计数，相对误差非常高，因此这需要一种具有接近恒定相对误差的技术，这种技术与 n 无关。

Morris 算法

抛硬币计数器的限制很明显，只能节省一半空间。

在这里，我们尝试利用对数的核心特性——对数函数的增长与指数函数成反比——这意味着对于较小的 n 值，值 v 增长得更快——提供更好的近似值。这确保了相对误差接近恒定，即与 n 无关，并且事件的数量是更少还是更多都无关紧要对于超大数可以使用对数简化

$$ \large 估算值v_{n} = \log_{e}(实际值n+1) $$

对数逆运算可以计算出估算值

$$ \large 实际值n_{v} = e^{估算值v}-1 $$

累加

还记得通过硬币的两面实现 0.5 的概率从而实现使用一半空间吗？ 这里为了确定我们是否应该增加 v 的值，如果 v 的变化导致 n 值的变化很大，那么我们增加 v 的概率应该较低，反之亦然。 我们将 d 定义为该跳跃的倒数，即对应于 v + 1 和 v 的 n 之间的差。

$$ \large d = \frac{1}{n_{v+1}-n_{v}} $$

d 的值将始终在区间 (0, 1) 中。两个n之间的跳跃越小，d的值越大，跳跃越大，d的值越小。这也意味着随着 n 的增加，d 的值会变得越来越小，这使得我们更难改变 v。

所以我们选择一个在区间 [0, 1) 中均匀生成的随机数 r 并使用这个随机数 r 和之前定义的 d 比较，如果这个 r 小于 d 则增加计数器 v 否则，我们保持原样。随着 n 的增加，d 会减少，这使得在 [0, d) 范围内选择 r 的几率变得更加困难

估算值 & 实际值

Morris 算法使用欧拉数为底的对数，估算值v的计算函数

$$ \large 估算值v = \frac{\log_{e}(实际值n+1)}{\log_{e}(2)} $$

$$ \large 实际值n = e^{\log_{e}(2) * 估算值v} - 1 $$

当我们绘制由 Morris 算法产生的值与实际事件数量的关系时，我们发现 Morris 算法确实为较小的 n 值生成了更好的近似值，但随着 n 的增加，绝对误差增加，但相对误差保持相当恒定。下面显示的插图描述了这些事实。

1000 计数估算

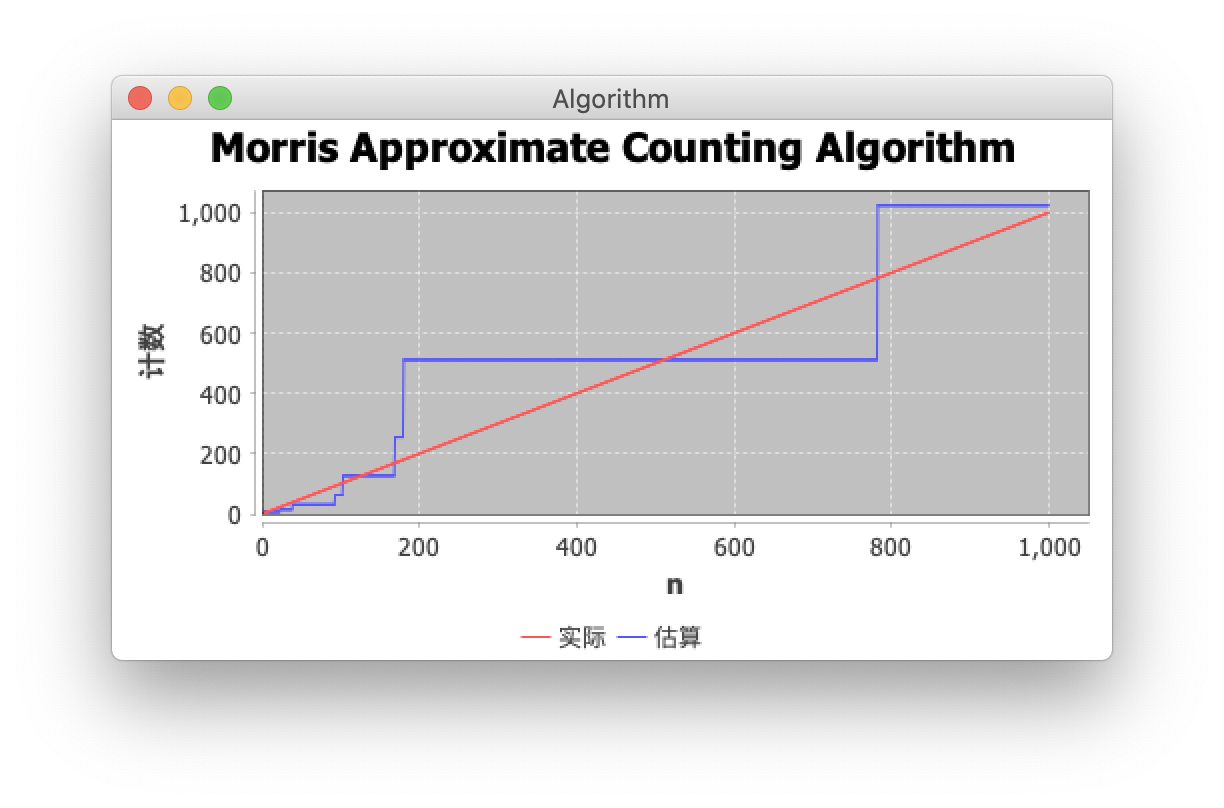
100万 计数估算

MorrisApproximateCounter.java

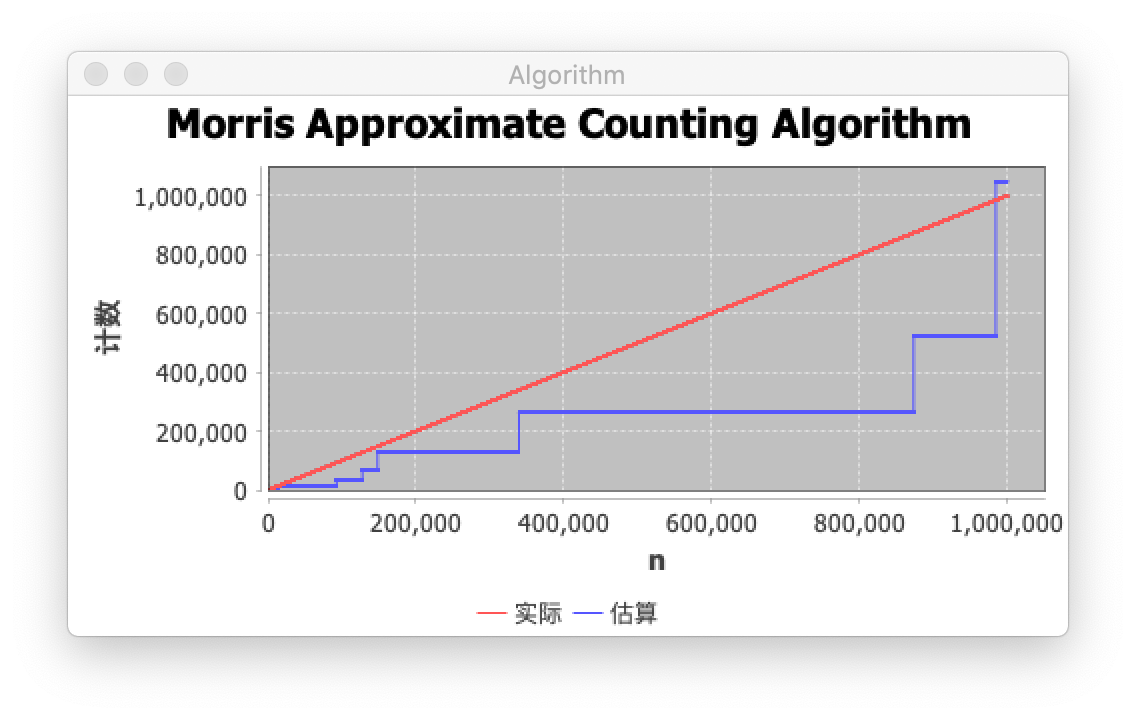
例如我们记录网页的访问数量，并给出热点排名，如果我们面对的是每天有数十亿的访问场景，那么十亿和十亿零几千万差别并不大。这时我们往往不需要精确计数，如果我们只需要得到计数的近似值，并且使用一个小的数据结构( 例如 1 byte) 作为计数器，那么我们只需要大概 2GB 的空间就足够了。

以下样例代码中，我们使用 1 byte (8bit) 的变量，实现千万级的计数

public class MorrisApproximateCounter {

  private static final Logger log = LoggerFactory.getLogger(MethodHandles.lookup().lookupClass());

  /**
   * 定义一个计数器变量
   */
  byte counter = 0;

  /**
   * 模拟抛硬币概率
   */
  Random random = new Random();

  /**
   * 返回计数值
   */
  public double get() {
    return Math.pow(Math.E, Math.log(2) * counter) - 1;
  }

  /**
   * 计数值累加
   */
  public byte increment() {
    double n_next = Math.pow(Math.E, Math.log(2) * counter+1) - 1;
    double n = Math.pow(Math.E, Math.log(2) * counter) - 1;
    double d = 1 / (n_next - n);
    if(random.nextDouble() < d){
      this.counter++;
    }
    return this.counter;
  }

  public static void main(String[] args) {
    MorrisApproximateCounter mc = new MorrisApproximateCounter();

    // 定义实际数量
    int realCount = 1000_000;

    double[][] real_graph_data = new double[realCount][2];
    double[][] approximate_graph_data = new double[realCount][2];

    for (int n = 0; n < realCount; n++) {
      // 累加计数
      mc.increment();

      real_graph_data[n][0] = n;
      real_graph_data[n][1] = n;

      approximate_graph_data[n][0] = n;
      approximate_graph_data[n][1] = mc.get();
    }

    // 输出实际计数 和 近似计数
    log.info("实际计数 {}, 近似计数 {}", realCount, (int) mc.get());

    // 绘制图形
    LineChartFrame chart = new LineChartFrame("Algorithm", "Morris Approximate Counting Algorithm",
        "n", "计数");
    chart.addXYSeries("实际", real_graph_data);
    chart.addXYSeries("估算", approximate_graph_data);
    chart.pack();
    chart.setVisible(true);
  }
}

执行结果，因为采用随机概率，所以每次估算的近似值都不同，有的时候误差还较大，如何减少这种误差？

实际计数 1000000, 近似计数 1048574

空间复杂度

为了计数到 n，Morris 算法使用对数 log(n)，因此从 0 到 log(n) 计数所需的位数通常是 log(log(n))，因此空间复杂度为 O(log log n)。

多计数器

这里演示了如何使用一个数组通过哈希定位索引存储多个计数器，可以参考 MorrisApproximateHashCounter.java

参考

• Approximate Counting Algorithm - Wikipedia
• Probabilistic Counting and Morris’ Algorithm - Texas A&M University